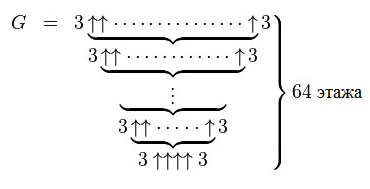
Возьмем три арифметических операции: 3 + 3, 3 x 3, 3 ^ 3 (последнее означает возведение в степень). Очевидно, что, помимо двух троек, в каждом из примеров незримо присутствует третье число. Это — порядок гипероператора. На протяжении двадцатого века в умах математиков витала идея выписать это скрытое число в явной форме. Дональд Кнут предложил заменить символ степени вертикальной стрелкой: 3 ↑ 3. Тогда следующая операция в последовательности, гипероператор–4, будет записываться как 3 ↑↑ 3. Нотация интуитивно понятна, но не очень удобна. Она не дает совершить концептуальный скачок.
Джон Конуэй решил сделать порядок гипероператора частью записи (собственно, это же раньше сделал Вильгельм Аккерман в своей функции Аккермана, но для гугологии ценнее способ Конуэя). В его стрелочной нотации возведение в степень записывается как 3 → 3 → 1, а уже следующий шаг (3 → 3 → 2) позволяет покинуть царство младших гипероператоров, так сказать, арифметические ясли, и вступить в гуголологический дворец.
И однако, как только первый шаг сделан, из интеллектуального режима мы снова возвращаемся в механический. Здесь я использую идею Дагласа Хофштадтера, который в книге «-Гёдель, Эшер, Бах»- предлагал разделять режим M и режим I- первый позволял механически исследовать некую формальную систему, второй — выходить за ее пределы. Не нужно творческого мышления, чтобы заменить третий член в записи Конуэя на двойку, тройку и так далее. Для галочки рассмотрим гипероператор–4, –5 и –6, чтобы напомнить, насколько быстро возрастают числа, а затем будем продвигаться дальше.
3 → 3 → 2
Это тетрация (термин Рубена Гудстайна). 3, тетрированное в 3, означает 3, дважды возведенное в степень 3:
(3 ^ (3 ^ 3)) = 3 ^ 27 = 7 625 597 484 987.
Только что мы совершили операцию, которая в дальнейшем будет уже недоступна: по рецепту действительно приготовили число. Получилось всего лишь семь с половиной триллионов, около половины ВВП США, сумма астрономическая, но для гуголологии это значит — детская. Тетрация позволяет нам из царства степеней перейти в царство степенных башен,
чье английское название — power towers — мгновенно пробуждает фантазию своими смысловыми коннотациями (это можно понять как «-башни могущества»- или «-башни энергии»-).
3 → 3 → 3
Это пентация. Джонатан Бауэрс предлагает называет число «-тритри»- (tritri). 3, пентированное в 3, — это 3, дважды тетрированное в 3, то есть 3, тетрированное в 3^3^3, то есть 3, возведенное в куб 7 625 597 484 987 раз. Если вы впервые знакомитесь с гуголологией, то на этом месте, в принципе, уже можно закончить. Мы получили нечто, чего достаточно для взрыва неподготовленного мозга: степенную башню из семи с половиной триллионов этажей.
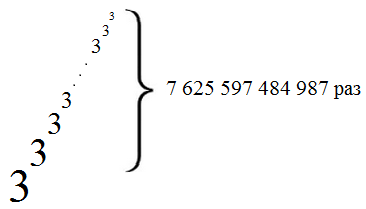
Число, для представления которого степенные башни становятся по большей части бесполезны. Это гексация. 3, гексированное в 3, — это 3, дважды пентированное в 3, то есть 3, пентированное в три 7 625 597 484 987 раз…- Нет, неверно. Дело в том, что при работе с большими числами нужно быть осторожным, чтобы не увлечься ложной поступательностью. Я использовал ход предыдущего этапа (манёвр предыдущей лиги), который здесь не годится. Нет, 3, дважды пентированное в 3, это 3, которое пентировано в 3 ( 3 → 3 → 3) раз. Здесь применимо то, что я говорил о «-рецептах рецептов»-. Сначала мы получаем рецепт тритри, описанный в предыдущем абзаце, а затем используем его, чтобы получить рецепт 3 → 3 → 4. Невообразимость снова скакнула вверх, мы снова оказались как бы в другом масштабе. Очаровательно, что, просто добавляя единицу, мы взлетаем на недосягаемые высоты, каждый раз всё более фантастические.
Замечу, что царство степенных башен плавно сменилось царством фигурных скобок. Чтобы записать пентацию, достаточно одной фигурной скобки, гексацию — двух, гипероператор–7 — трех и так далее. При этом мы будем обращаться уже не только со степенными башнями, но и с тетрационными башнями, пентационными, гексационными и так далее.
Каждый шаг в прогрессии гипероператоров невообразимо больше предыдущего, и однако эти шаги тривиальны. Нотация Конуэя позволяет нам сделать менее тривиальный шаг, просто добавив еще одну стрелку:
3 → 3 → 2 → 2
К сожалению, на данном этапе разнообразные наглядные способы представления теряют силу. Но приблизительно происходит следующее: если третье число в цепочке как бы говорит, что делать с первыми двумя (3 → 3 → 1: возьмите первые два числа и возведите одно из них в степень другого- 3 → 3 → 2: возьмите первые два числа и заставьте их проделывать операцию возведения в степень 3 раза- 3 → 3 → 3: возьмите первые два числа и заставьте их проделать тетрацию (3 → 3) раз), то четвертое обращает мощь всех чисел на них самих:
3 → 3 → 2 → 2 = 3 → 3 → ( 3 → 3 → 1 → 2) → 1 = 3 → 3 → (3 → 3) = 3 → 3 → 27
Уже здесь сложно уследить за руками. Мы рассмотрели несложную цепочку из четырех элементов — и сразу получили гипероператор–27. Осталось всего несколько шагов — и мифическое число Грэма останется позади.
3 → 3 → 3 → 3
Это число иногда называют «-тетратри Конуэя»-. Еще раз отмечу: хотя мы уже очень, очень далеко ушли от любого здравого определения здравого смысла, мы по–прежнему работаем в режиме М, то есть просто наращиваем мощь нотации. Нет никаких проблем с тем, чтобы добавить пятое звено в цепочке, шестое, седьмое. Каждый раз понадобится время, чтобы понять, как расшифровать полученный рецепт, и тем не менее процедура тривиальна.
Что же делает Джонатан Бауэрс? Он смотрит на нотацию Конуэя и как бы говорит: «-Нет, это слишком медленно. Вот если бы четвертое число указывало количество стрелочек!»-

{3, 3, 3}
Тройные массивы Бауэрса полностью идентичны тройным цепочкам Конуэя.
{3, 3, 3} = 3 → 3 → 3 = 3 ^ (3 ^ (3 ^ (3 ^…- 7 625 597 484 987 раз…- ^ 3) ^ 3) ^ 3)
Однако при добавлении четвертого элемента вдруг происходят странные вещи. Бауэрс находит способ раздувать свой массив максимально возможным образом. Творческий шаг, который он делает, — это не кодирование стрелок Конуэя в четвертом числе, а нечто гораздо более эффективное.
Точно так же, как перед переходом к тетрации нам нужно было идентифицировать в записи «-3 x 3″- или «-3^3″- некое третье число (порядок гипероператора), так же и здесь нужно понять, какая часть формализма до сих пор принималась за данность. Нельзя ли ее выписать отдельно? Квантифицировать? Проще говоря, где кроется возможность для продолжения вечеринки? Мы смотрим на {3, 3, 3} и видим три числа, но где притаилось четвёртое? Бауэрс отвечает: посчитайте количество пар фигурных скобок.
{3, 3, 3} = {3, 3, 3, 1}.
{3, 3, 3, 2} = {{3, 3, 3}}.
Фактически, мы только что сломали предыдущую систему записи. Мы нарушили правила. Никто не говорил, что скобки можно удваивать! Но никто и не говорил, что нельзя! Как в детской игре, когда один ребенок кричит другому: «-Эй, мы так не договаривались!»- А другой отвечает: «-Мы просто не обсуждали это правило»-.
Важное пояснение: у нотации Бауэрса есть две версии. {3, 3, 2} можно записать как 3 {2} 3. Для трехчленного массива это кажется путаницей (так как третье число, порядок гипероператора, оказалось вдруг вторым в записи: {a, b, c} = a {c} b). Логика такова, что мы берём два числа (по краям) и что–то с ними делаем — что именно, указано в центре. При введении четвертого члена полезно держать в уме оба способа записи.
Итак, общее правило таково (Бауэрс приводит его в ранней о своей системе):
{a, b, 1, 2} = a {{1}} b = a { a { a…-.a { a { a } a } a…-. a } a } a
(где количесто а, расходящихся от центра к краям, равно b)
Стиль самого Бауэрса слишком лаконичен, поэтому дальше я процитирую из Криса Бёрда, который гораздо лучше раскладывает все по полочкам.
a {{1}} 2 = a {a} a
a {{1}} 3 = a {a {a} a} a
a {{1}} 4 = a {a {a {a} a} a} a
В статье Бёрда сравниваются нотации Конуэя и Бауэрса и показывается, как вторая обходит первую. Если у Конуэя единица на третьем месте мешает числу расти:
3 → 3 → 1 → 2 = 3 → 3,
то у Бауэрса этого не происходит:
{3, 3, 1, 2} = 3 {{1}} 3 = 3 {3 {3} 3} 3 = {3, 3, {3, 3, 3}} = {3, 3, тритри}
Мы мгновенно получили безумное число с гипероператором порядка тритри. Проведем еще одно сравнение. У Конуэя, как мы видели:
3 → 3 → 2 → 2 = 3 → 3 → ( 3 → 3 → 1 → 2) → 1 = 3 → 3 → (3 → 3) = 3 → 3 → 27
У Бауэрса:
{3, 3, 2, 2} = 3 {{2}} 3 = 3 {{1}} 3 {{1}} 3 = {3, {3, 3, тритри}, 1, 2} =
= 3 {3 {3…- 3 {3 {3} 3} 3…- 3} 3} 3
(где количесто 3, расходящихся от центра к краям, равно {3, 3, тритри} )
Получается, что там, где у Конуэя меняется третье число, у Бауэрса — второе, причем гораздо более кардинально. У Конуэя четвертое число скармливает всю цепочку третьему числу- у Бауэрса — второму. Вся мощь формулы обращается сама на себя, и отбрасывать двойные скобки не разрешается, пока не будет исчерпан сумасшедший лимит.
Стоит ли говорить, что при утроении, учетверении и так далее фигурных скобок происходит скачкообразный рост умопомрачительности. На странице с Бесконечноскрёбами об этом говорят все более эмоциональные и игривые комментарии Бауэрса к очередным монстрам. Про число «-боггол»- (boggol), которое содержит шестерные скобки и равняется {10, 10, 100, 6}, он пишет: «-Boggles the mind doesn’-t it»- («-Поражает, не так ли?»-). Нормой становятся возгласы вроде «-GOLLY TELLY it’-s huge!»- (Что–то вроде: «-Мама дорогая, вот так громадина!»-)
Замечательный результат Криса Бёрда заключается в том, что массив Бауэрса всего из четырех элементов (то есть кварталы с шестого по десятый) позволяет легко вместить в себя всю нотацию Конуэя:
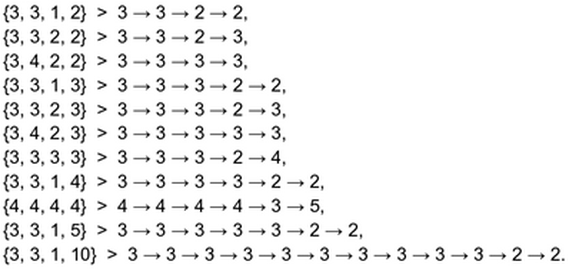
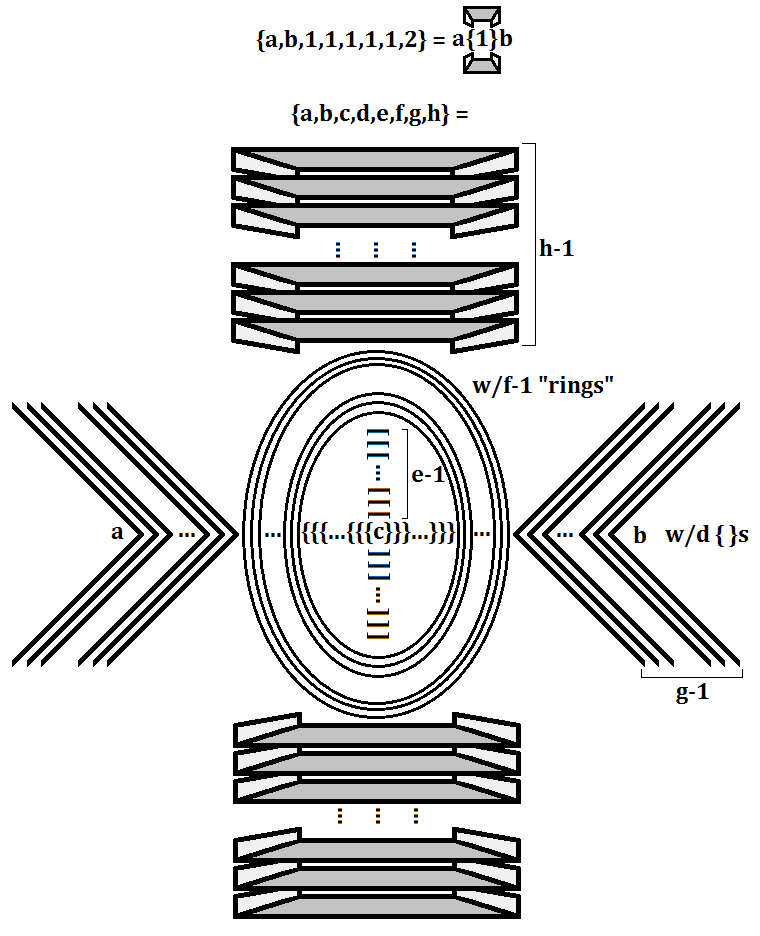
Наконец, приведя в 13–м квартале число ультатри:
{3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3}, —
с 27–ю тройками, Бауэрс замечает: «-Мы дошли до предела прочности линейных массивов»-.
Итак, что дальше? Есть ли возможность еще раз взглянуть на простую запись {3, 3, 3} и выжать из этого формализма еще какую–нибудь интуицию? Бауэрс обращает внимание на запятые между числами и принимает каждую из них за дополнительные числа, которые обозначают, в каком измерении продолжается массив. Обычная запятая — это (0), массив не меняет измерение. Но как только мы пишем между числами (1), это значит переход на следующую строчку. (2) обозначает переход в следующую плоскость. Таким образом, квадрат из троек («-дутритри»-) записывается так:
{3, 3, 3 (1) 3, 3, 3 (1) 3, 3, 3}
Куб из троек («-диментри»-) так:
{3, 3, 3 (1) 3, 3, 3 (1) 3, 3, 3 (2) 3, 3, 3 (1) 3, 3, 3 (1) 3, 3, 3 (2) 3, 3, 3 (1) 3, 3, 3 (1) 3, 3, 3}
Мы благополучно добрались до 18–го квартала. В конце 19–го Бауэрс замечает: «-Эти числа начинают вырываться из плоскостных массивов»-. Линейные, плоскостные, на очереди — объемные.
В 22–м классе вечноскрёбов встречает число «-дулатри»- и расширение нотации:
{3, 3 (0, 1) 2} = 3^3 &- 3 (где &- означает «-массив из»-)
Теперь в обычных скобках может стоять два числа. Если многомерные массивы можно назвать «-экспоненциальным»- (степенными), так как они задавались числом в некой степени, то новые массивы — «-тетрациальные»-, так как задаются тетрированным числом. Может показаться, что это просто супер–измерения (super–dimensions), некие измерения в квадрате. На самом деле тетрациальные массивы включают «-супер–измерения»-, «-тризмерения»-, «-квадризмерения»- и так далее («-super dimensions, trimensions, quadramensions»-). Каждый новый класс настолько же мощен, как и обычные измерения — то есть, простите, невообразимо мощнее.
Чтобы проиллюстрировать эту идею, Бауэрс пишет: «-Пусть R представляет линию (R обозначает множество действительных (Real) чисел, расположенных вдоль прямой). Тогда R^3 = 3 измерения, R^R = R^R^1 — первое супер–измерение, R^R^4 = 4 супер–измерения. R^R^R = R^R^R^1 = первое тризмерение»-. В конце этой цитаты американец делает удивительную вещь: он выражает само измерение при помощи своей нотации: «-R^R^R = R, тетрированное в 3, = {R, 3, 2}»-.
Пример массива в «-тризмерении»- — число «-триментри»- из 24–го квартала:
{3, 3 (0, 0, 0, 1) 2}
Как поясняет Бауэрс, это массив из троек, расположенный в «-тризмерении»-, то есть в измерении измерений измерений. Иначе говоря, нужно взять тройки, забить ими сначала наши три измерения, затем все многомерные миры, затем выйти в супер–измерения — заполнить все много–супер–мерные миры, и только затем остановиться.
В 26–м квартале Бесконечноскрёбов, представляющим собой высшие примеры тетрациальных массивов, встречается, возможно, мой любимый неологизм Бауэрса: «-гоппатот»- (goppatoth), который прекрасно звучит и выглядит на обоих языках. Гоппатот записывается так:
{10, 100, 2} &- 10
То есть {10, 100, 2}–массив десяток, или же 10^^100–массив десяток. Нужно 100 раз возвести десять в десятую степень, построить решетку с таким количеством ячеек (причем она будет находиться в стозмерении, то есть измерении измерений измерений…-измерений (слово повторено сто раз)), затем заполнить все ячейки десятками — и только тогда можно приниматься решать этот массив.
Стоит ли говорить, что за тетрациальными массивами идут пентациальные, где встречается смешное число «-кунгулус»-, и «-высшие операциональные»-, где нас ждут «-тридекатрикс»- и кошмарный «-голапулус»-: {10,100} &- 10 &- 10 = {10,10 (100) 2} &- 10 = (гуголовый массив десяток)–массив десяток).
В тридцатом квартале Бесконечноскрёбов мы покидаем царство всего, к чему применимо слово «-измерение»-, и идем дальше.
{3, 3 / 2} = 3 &- 3 &- 3 = {3, 3, 3} &- 3
(пентациональный массив из «-тритри»- элементов)
«-Легион»- позволяет создавать безумные вереницы из амперсандов. Так, Большая Бува из того же класса, что и «-триакулус»-, выглядит следующим образом:
{3, 3, 3 / 3} = {3 &- 3 &- 3 / 2}
То есть на этот раз «-тритри»- — это не количество элементов в нашем массиве, а количество элементов в цепочке 3 &- 3 &-…- &- 3 &- 3.
Не думаю, что удивлю кого–то, если скажу, что каждый легион может быть многомерным, тетрациональным, пентациональным и так далее (то есть нужно представить себе массив из косых черт, распространяющийся во всех измерениях). Число «-Букуваха»- из 34–го квартала выглядит следующим образом:
{100,100 A 2}
(где A — 100^100–массив из легионных знаков (стомерный массив))
Остался всего один шаг до финального числа, однако этот шаг, как водится у Бауэрса, феноменально огромен. Математик вводит символ @ (a @ b обозначает «-легионный массив размера a из b»-) и обратный слэш :
{a,b 2} = a @ a @ a…- a @ a @ a (где а повторяется b раз)
При этом называется «-лугионный знак»-, от которого мы легко можем перейти к лугионным полям и лугионным массивам, а также знаку «-лугионный массив из»- — %, который, в свою очередь, называется л а гионным знаком. Скоро мы приходим к л э гионам (|) и л и гионам (–). (В царстве лугионов встречается смешное число «-гошомити»- («-гошомитство»-): {100, 100 …- 2} (где 100 лугионных знаков )).
Последний квартал — тридцать пятый и состоит из двух чисел. Чтобы их назвать, нужно определить L как прогрессию из легионов, лугионов, лагионов, лэгионов и лигионов: L1, L2, L3…- Далее идут LL (L x L), LLL, LLLL и так далее. Также нужно учесть такую нотацию с нижними индексами:
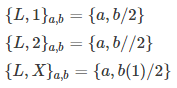
Изобретатель идет от известного к неизвестному. Он видит некие пути, по которым еще никто не ходил, но он не видит и не может видеть новые способы передвижения — экстраполяцию самой ходьбы, ее переизобретение. На каждом этапе своей нотации Бауэрс пытался не просто пойти дальше, а пойти вбок, при этом используя то, что уже есть под рукой. Вместе со своими «-гонгулусами»- и «-гоппатотами»- он заражает детским восхищением перед возможностями взрослого разума.
Что еще почитать о гуголологии (по–английски):
1.Ресурс Роберта Мунафо, с которого для меня началась гуголология:
2. Энциклопедия гуголологии:
3. Статья Сбийса Сайбиана про Бауэрса (незаконченна):
4. Статья Криса Бёрда, в которой наиболее доступно сравниваются различные нотации:
5. Сайт Джонатана Бауэрса:
-
-
Ну и еще что нибудь настолько научного, что возможно и не пригодится уже нашей цивилизации : вот например , а вот и . Почитайте еще про и
-

| « Январь 2026 » | ||||||
|---|---|---|---|---|---|---|
| Пн | Вт | Ср | Чт | Пт | Сб | Вс |
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | |